-
Faculty of Science, Department of Applied Mathematics
- Professor
- Michiyuki WATANABE
- Research Field
Mathematics, Analysis, Mathematical Physics
- Keyword(s)
Partial differential equations, Scattering theory, Inverse problems
- Research theme
-
- Inverse problems for partial differential equations
- Nonlinear waves and partial differential equations
- Scattering theory and its relevance to the elastic wave equation for seismic waves
Outline of research activities



My research explores the mathematical connections between quantum mechanical scattering, nonlinear waves, and seismic waves to understand how mathematical methods and analysis can potentially gain new insights and develop novel approaches.
Finding and understanding the mathematical connections that exist between different fields and phenomena is what makes mathematical research so fascinating.- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Professor
- Shintaro KUROKI
- Research Field
Transformation groups, Toric topology
- Keyword(s)
Group action, (Equivariant) Cohomology, Graph
- Research theme
-
- Cohomological rigidity problem
- Application of GKM theory to geometry
- Classification problem of the spaces with group actions, etc.
Outline of research activities





In the word of mathematics, the symmetric structures on spaces are described by groups.
We call such symmetric space a space with group action.
My research interest lies in geometry and topology of the spaces with torus actions.
In this decades, the area so-called toric topology has been emerged.
Roughly speaking, toric topology can construct bridges among different areas (geometry, algebra and combinatorics) by the study of the spaces with torus actions.
In the near future, I would like to continue to study toric topology more deeply and challenge to solve open problems.
- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Professor
- Shinzo BANNAI
- Research Field
Algebraic Geometry
- Keyword(s)
Algebraic Curves, Surfaces, Galois Covers, Gröebner Bases
- Research theme
-
- Classification of the embedded topology of plane curves
- Geometric inverse Galois problem and its applications
- Computational aspects of Algebraic Geometry
Outline of research activities


Algebraic Geometry is a field in mathematics that studies geometric objects defined by polynomials. Since polynomials are used in the definition, algebraic methods can be used to study the geometry.
The main objects that I am interested in are rlow dimensional objects such as algebraic curves and surfaces. I try to find “invariants” that can be used to distinguish similar curves, thnik of the “exsitence problem” which asks wheter curves satisfying given conditions exist, and once we know the existance, considr the “construction problem” in which the goal is to explicitely write down the equation. Since explicit equations appear, I sometimes use computers in order to execute my calculations.- Desired cooperation
-
- -
-
Faculty of Science, Department of Applied Mathematics
- Professor
- Takahiro AOYAMA
- Research Field
Measure Theory, Probability Theory, Analytic Number Theory
- Keyword(s)
Discrete Distribution, Multiple Zeta Function
- Research theme
-
- Discrete distributions and multiple zeta functions
- Random walks on graphs
- Stochastic processes
Outline of research activitiesIn general, we have less mathematical theories of multidimensional discrete measures than those of one dimensional discrete and continuous measures, and multidimensional continuous measures. As to develop a new theory of multidimensional discrete measures, we have shown that many kinds of them can be written by our multiple zeta functions. Especially, we are interested in looking for a new theory of discrete measures with infinite supports. We are also interested in some probabilistic applications such as random walks on graphs.
- Desired cooperation
-
- Data science
- Machine learning
- Mathematical finance
-
Faculty of Science, Department of Applied Mathematics
- Professor
- Takashi OHE
- Research Field
Inverse problems
- Keyword(s)
Inverse problems, Numerical Analysis, Differential equations
- Research theme
-
- Mathematical and numerical analysis of inverse source problems of wave equations
- Mathematical and numerical analysis of inverse scattering problems
- Mathematical and numerical analysis of abnormal diffusion process
Outline of research activities
Inverse problem can be found in various fields, for examples, X-ray CT in medical fields, and non-destructive evaluations in engineering fields.In our laboratory, we make a mathematical analysis of inverse problems, especially, inverse source problems for wave equations and inverse scattering problems. We develop a numerical procedure to apply our mathematical results to practical problems.
We also study mathematical and numerical analysis for abnromal diffusion process in the soil.
- Desired cooperation
-
- Mathematical and numerical analysis for evaluation of wave sources or pollusion sources
- Mathematical and numerical analysis for non-destructive or non-invasive evaluation.
-
Faculty of Science, Department of Applied Mathematics
- Professor
- Yoshinori HAMAHATA
- Research Field
Algebra, Number Theory
- Keyword(s)
Dedekind sums, zeta functions, function fields
- Research theme
-
- Dedekind sums and their applications
- Special values of Dirichlet series
- Number theory in function fields.
Outline of research activities

There are analogies between algebraic number fields and function fields of one variable over finite fields. Number theory has developed on both fields. Using Dedekind sums which are special numbers, I study functions in number theory – zeta functions, L-functions, Dirichlet series, modular forms, and modular functions, for example. Using these functions, I also study numbers.
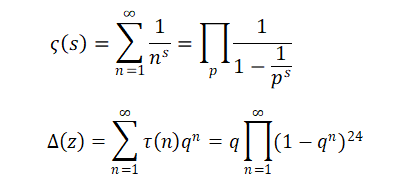
- Desired cooperation
-
- Function fields and finite fields.
-
Associate professor, Department of Applied Mathematics
- Associate professor
- Hiraku ABE
- Research Field
Geometry, Topology, Transformation groups
- Keyword(s)
Algebraic varieties, group actions, cohomology rings
- Research theme
-
- Algebraic varieties with group actions
- Hessenberg varieties
- Flag varieties and toric varieties
Outline of research activities

The main theme for my research in mathematics is “spaces with symmetry”. I am particularly interested in the field in which algebra, geometry, and combinatorics (three different kinds of mathematics!) intersect all at once. For those area of mathematics, it is often happens that a single phenomenon has many ways to be viewed; it can have geometric interpretaions, representation theoretic interpretations, and combinatorial representaions. Through these experience, we can feel the richness of mathematics. In particular, it is exceptional when we can express abstract geometric/topological quantities in terms of concrete algebra and combinatorics. Recently,I am particularly interested in the geoemetry and topology of Hessenberg varieties.
- Desired cooperation
-
- None
-
Faculty of Science, Department of Applied Mathematics
- Associate professor
- Kimiko YAMADA
- Research Field
Moduli spaces in algebraic geometry
- Keyword(s)
moduli, birational geometry, singularities, Kodaira dimension
- Research theme
-
- moduli spaces of vector bundles on algebraic surfaces
- singularities of moduli
- Kodaira dimension of moduli
Outline of research activities



My field of expertise is algebraic geometry. There we consider a set of zero points (algebraic variety) of polynomials. For example, lines, circles, hyperbolas, and parabolas are algebraic varieties. The set of all geometric objects with certain properties is called a moduli space.
Moduli spaces of stable vector bundles on complex algebraic surfaces X are actively investigated as concrete examples of algebraic varieties.For an algebraic variety M, the Kodaira dimension is determined.
The Kodaira dimension of M is an important invariant related to the curvature of M. Also, there is the minimal model theory to understand higher dimensional varieties. In this theory, one simplifies a variety by exploding and contracting its subspaces to get a simple variety, called minimal model.I am interested in singularities, the Kodaira dimenson and the minimal model program of moduli space M.
(1) For large classes of surfaces X, I described the minimal model program of M by using words of moduli theory.
(2) I examined singularities of M, and in case where the structure of X is relatively simple, I showed that singularities of M are “good”. As a result, I calculated the Kodaira dimension of M.- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Associate professor
- Kiyokazu SUTO
- Research Field
Representation theory, Computer aided education and research system
- Keyword(s)
Lie algebra, Lie group, Representation theory, Network,Virtualization
- Research theme
-
- Representations of Lie groups and Lie algebras
- Development of computer aided education and research systems by making use of virtualization
Outline of research activities
Construction and analysys of representations of mainly infinite dimesional Lie groups and Lie algebras.
Development of computer aided education and research system by making use of virtualization. It can be maintained safely and applicative to many fields, thanks to virtualization.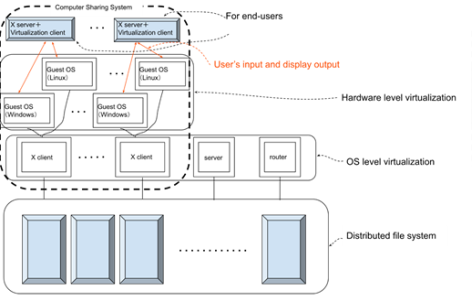
- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Associate professor
- Kota URIYA
- Research Field
Partial differential equations
- Keyword(s)
Nonlinear dispersive equations, Fourier Analysis
- Research theme
-
- Global behavior of the solution to the nonlinear Schrödinger eq.
- Blow-up of the solution to the Nonlinear Schrödinger eq.
- Functional inequalities
Outline of research activitiesWe study the local well-posedness of the initial value problem and the asymptotic behavior of the solution to nonlinear Schrodinger equations by means of harmonic analysis and functional analysis. Our particular concern is that how the coefficients of the linear principal part influence the global behavior of the solution to nonlinear Schrodinger equations. This is purely from the mathematical point of view but our another aim is to analyze real physical phenomena based on mathematical theories.

- Desired cooperation
-
- Physical models arise in nonlinear optics
-
Faculty of Science, Department of Applied Mathematics
- Associate professor
- Masakazu ONITSUKA
- Research Field
Qualitative theory of ordinary differential equations
- Keyword(s)
Ordinary differential equations, Qualitative theory, Stability
- Research theme
-
- On the stability of nonautonomous ordinary differential equations
Outline of research activities





The field of my research is part of the qualitative theory of ordinary differential equations. In this research, we focus on the behavior of all solutions of nonautonomous ordinary differential equations. How does the variable coefficients of ODE influence the stability of the solutions? The main purpose of this research is to answer this question. In particular, we deal with the problem on the stability in the Lyapunov sense. For example, we treat asymptotic stability, uniform asymptotic stability and exponential stability. By understanding these essence, we aim to contribute to the development of ODE.
- Desired cooperation
-
- Applications to control theory
-
Faculty of Science, Department of Applied Mathematics
- Associate professor
- Yoshiyuki MORI
- Research Field
Graph Theory and Representation Theory of Finite Groups
- Keyword(s)
Graph Theory, Representation Theory
- Research theme
-
- Representation Theory of Finite Groups
- Knot and Link
- Number Theory with a Computer
Outline of research activities

Determination and characterization of the structure of graphs.
Recognition of graph isomorphism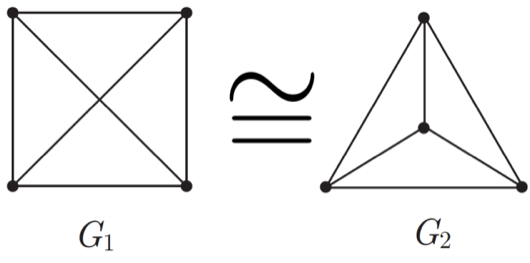
The study of Polynomial Invariants of Knots and Links
- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Lecturer
- Masateru INOUE
- Research Field
Topology
- Keyword(s)
Homotopy theory
- Research theme
-
- Hit problem
Outline of research activities

I am interested in hit problem. The Steenrod algebra acts on polynomial algebras over the field of two elements. Hit problem is to find a minimal generating set of polynomials over the Steenrod algebra. General linear groups act on polynomial algebras, and this commutes with the action of the Steenrod algebra. These are motivated by problems in topology, I consider this problem from various viewpoints.
- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Assistant professor
- Taiki SHIBATA
- Research Field
Algebraic Groups, Lie Theory and Representation Theory
- Keyword(s)
Hopf Algebras, Algebraic Supergroups, Lie Algebras, Modular Representions, Supersymmetry
- Research theme
-
- A Hpof algebraic approach to the study of algebraic supergroups
- Supermathematics and its applications to non-supermathematics
- Modular representation theory
Outline of research activities
My research interests are in the area of supermathematics.
In general, the structures of algebraic groups G are complicated. However, it is known that the “tangent space” Lie(G) of G which naturally forms a Lie algebra strongly reflects many properties of G. In positive characteristic, one should use the hyperalgebra hy(G) of G which is a refinemt of the notion of Lie(G) and forms a Hopf algebra.
As a super-analogue of algebraic groups (resp. Lie algebrs), algebraic supergroups (resp. Lie superalgebras) play an imprtant role not only in theoretical physics but also in mathematics. I proved that the above phenomena holds in super-world. Moreover, I showed that a Hopf algebraic approach is effective to study representations of algebraic supergroups. I would like to apply the results to study modular representations of algebraic supergroups and contribute to non-supermathematics.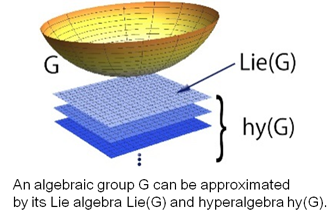
- Desired cooperation
-
- Theoretical Phsics (Supersymmetry, Conformal field theory etc.)





