-
Faculty of Science, Department of Applied Mathematics
- Professor
- Shintaro KUROKI
- Research Field
Transformation groups, Toric topology
- Keyword(s)
Group action, (Equivariant) Cohomology, Graph
- Research theme
-
- Cohomological rigidity problem
- Application of GKM theory to geometry
- Classification problem of the spaces with group actions, etc.
Outline of research activities





In the word of mathematics, the symmetric structures on spaces are described by groups.
We call such symmetric space a space with group action.
My research interest lies in geometry and topology of the spaces with torus actions.
In this decades, the area so-called toric topology has been emerged.
Roughly speaking, toric topology can construct bridges among different areas (geometry, algebra and combinatorics) by the study of the spaces with torus actions.
In the near future, I would like to continue to study toric topology more deeply and challenge to solve open problems.
- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Professor
- Shinzo BANNAI
- Research Field
Algebraic Geometry
- Keyword(s)
Algebraic Curves, Surfaces, Galois Covers, Gröebner Bases
- Research theme
-
- Classification of the embedded topology of plane curves
- Geometric inverse Galois problem and its applications
- Computational aspects of Algebraic Geometry
Outline of research activities


Algebraic Geometry is a field in mathematics that studies geometric objects defined by polynomials. Since polynomials are used in the definition, algebraic methods can be used to study the geometry.
The main objects that I am interested in are rlow dimensional objects such as algebraic curves and surfaces. I try to find “invariants” that can be used to distinguish similar curves, thnik of the “exsitence problem” which asks wheter curves satisfying given conditions exist, and once we know the existance, considr the “construction problem” in which the goal is to explicitely write down the equation. Since explicit equations appear, I sometimes use computers in order to execute my calculations.- Desired cooperation
-
- -
-
Faculty of Science, Department of Applied Mathematics
- Professor
- Yoshinori HAMAHATA
- Research Field
Algebra, Number Theory
- Keyword(s)
Dedekind sums, zeta functions, function fields
- Research theme
-
- Dedekind sums and their applications
- Special values of Dirichlet series
- Number theory in function fields.
Outline of research activities

There are analogies between algebraic number fields and function fields of one variable over finite fields. Number theory has developed on both fields. Using Dedekind sums which are special numbers, I study functions in number theory – zeta functions, L-functions, Dirichlet series, modular forms, and modular functions, for example. Using these functions, I also study numbers.
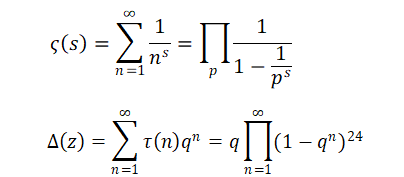
- Desired cooperation
-
- Function fields and finite fields.
-
Associate professor, Department of Applied Mathematics
- Associate professor
- Hiraku ABE
- Research Field
Geometry, Topology, Transformation groups
- Keyword(s)
Algebraic varieties, group actions, cohomology rings
- Research theme
-
- Algebraic varieties with group actions
- Hessenberg varieties
- Flag varieties and toric varieties
Outline of research activities

The main theme for my research in mathematics is “spaces with symmetry”. I am particularly interested in the field in which algebra, geometry, and combinatorics (three different kinds of mathematics!) intersect all at once. For those area of mathematics, it is often happens that a single phenomenon has many ways to be viewed; it can have geometric interpretaions, representation theoretic interpretations, and combinatorial representaions. Through these experience, we can feel the richness of mathematics. In particular, it is exceptional when we can express abstract geometric/topological quantities in terms of concrete algebra and combinatorics. Recently,I am particularly interested in the geoemetry and topology of Hessenberg varieties.
- Desired cooperation
-
- None
-
Faculty of Science, Department of Applied Mathematics
- Associate professor
- Kimiko YAMADA
- Research Field
Moduli spaces in algebraic geometry
- Keyword(s)
moduli, birational geometry, singularities, Kodaira dimension
- Research theme
-
- moduli spaces of vector bundles on algebraic surfaces
- singularities of moduli
- Kodaira dimension of moduli
Outline of research activities



My field of expertise is algebraic geometry. There we consider a set of zero points (algebraic variety) of polynomials. For example, lines, circles, hyperbolas, and parabolas are algebraic varieties. The set of all geometric objects with certain properties is called a moduli space.
Moduli spaces of stable vector bundles on complex algebraic surfaces X are actively investigated as concrete examples of algebraic varieties.For an algebraic variety M, the Kodaira dimension is determined.
The Kodaira dimension of M is an important invariant related to the curvature of M. Also, there is the minimal model theory to understand higher dimensional varieties. In this theory, one simplifies a variety by exploding and contracting its subspaces to get a simple variety, called minimal model.I am interested in singularities, the Kodaira dimenson and the minimal model program of moduli space M.
(1) For large classes of surfaces X, I described the minimal model program of M by using words of moduli theory.
(2) I examined singularities of M, and in case where the structure of X is relatively simple, I showed that singularities of M are “good”. As a result, I calculated the Kodaira dimension of M.- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Associate professor
- Kiyokazu SUTO
- Research Field
Representation theory, Computer aided education and research system
- Keyword(s)
Lie algebra, Lie group, Representation theory, Network,Virtualization
- Research theme
-
- Representations of Lie groups and Lie algebras
- Development of computer aided education and research systems by making use of virtualization
Outline of research activities
Construction and analysys of representations of mainly infinite dimesional Lie groups and Lie algebras.
Development of computer aided education and research system by making use of virtualization. It can be maintained safely and applicative to many fields, thanks to virtualization.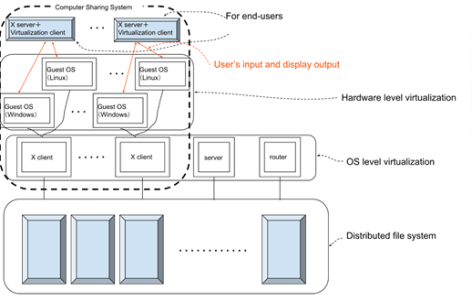
- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Associate professor
- Yoshiyuki MORI
- Research Field
Graph Theory and Representation Theory of Finite Groups
- Keyword(s)
Graph Theory, Representation Theory
- Research theme
-
- Representation Theory of Finite Groups
- Knot and Link
- Number Theory with a Computer
Outline of research activities

Determination and characterization of the structure of graphs.
Recognition of graph isomorphism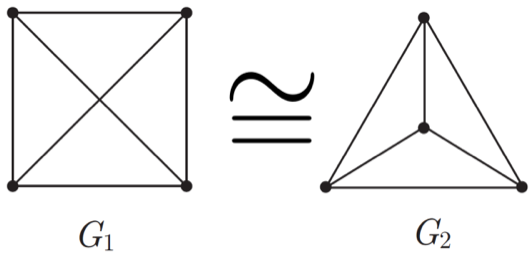
The study of Polynomial Invariants of Knots and Links
- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Lecturer
- Masateru INOUE
- Research Field
Topology
- Keyword(s)
Homotopy theory
- Research theme
-
- Hit problem
Outline of research activities

I am interested in hit problem. The Steenrod algebra acts on polynomial algebras over the field of two elements. Hit problem is to find a minimal generating set of polynomials over the Steenrod algebra. General linear groups act on polynomial algebras, and this commutes with the action of the Steenrod algebra. These are motivated by problems in topology, I consider this problem from various viewpoints.
- Desired cooperation
-
-
Faculty of Science, Department of Applied Mathematics
- Assistant professor
- Taiki SHIBATA
- Research Field
Algebraic Groups, Lie Theory and Representation Theory
- Keyword(s)
Hopf Algebras, Algebraic Supergroups, Lie Algebras, Modular Representions, Supersymmetry
- Research theme
-
- A Hpof algebraic approach to the study of algebraic supergroups
- Supermathematics and its applications to non-supermathematics
- Modular representation theory
Outline of research activities
My research interests are in the area of supermathematics.
In general, the structures of algebraic groups G are complicated. However, it is known that the “tangent space” Lie(G) of G which naturally forms a Lie algebra strongly reflects many properties of G. In positive characteristic, one should use the hyperalgebra hy(G) of G which is a refinemt of the notion of Lie(G) and forms a Hopf algebra.
As a super-analogue of algebraic groups (resp. Lie algebrs), algebraic supergroups (resp. Lie superalgebras) play an imprtant role not only in theoretical physics but also in mathematics. I proved that the above phenomena holds in super-world. Moreover, I showed that a Hopf algebraic approach is effective to study representations of algebraic supergroups. I would like to apply the results to study modular representations of algebraic supergroups and contribute to non-supermathematics.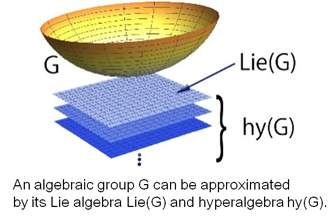
- Desired cooperation
-
- Theoretical Phsics (Supersymmetry, Conformal field theory etc.)
-
Faculty of Science, Department of Applied Science
- Professor
- Takanobu KAMATAKI
- Research Field
sedimentology, natural disaster, disaster education
- Keyword(s)
tsunami deposit, flood deposit, natural disaster, disaster education
- Research theme
-
- Study on paleo-tsunami history and inundation in coastal lowland area
- Study on disaster assessment based on tsunami and flood deposits
Outline of research activities



Tsunami deposits are useful in attempted reconstructins of prehistoric tsunamis. Geological analyses of tsunami deposits can provide estimates of several parameters of tsunamis, such as recurrence intervals and inundation areas. To assess the history of paleotsunami, we investigate the tsunami deposits around the coastal lowlands on the eastern margin of the Sea of Japan. These studies provides useful information for advancing tsunami disaster risk assessment in coastal lowlands.
In addition, we are active in the practice of disaster education.- Desired cooperation
-
- tsunami and flood survey
- disaster education
-
Faculty of Science, Department of Applied Science
- Professor
- Yutaka NAGABUCHI
- Research Field
Analysis (Functional Differential Equations and Integral Equations )
- Keyword(s)
Functional Differential Equations, Integral Equations, Dynamics of solutions, Stability, Center manifolds
- Research theme
-
- Asymptotic properties of solutions (e.g. stability, peiodicity)
- Theory of center manifolds and analysis of dynamics of solutions
- Bifurcations of solutions
Outline of research activities
My research interests are in the area of differential equations, functional differential (or difference) equations and integral equations with infinite delay. We have established linear theory for these equations via functional analytic methods; and now develop theory of invariant manifolds, specifically center manifolds, together with theory of bifurcation structure of solutions.
- Desired cooperation
-
- Differential equations, functional differential equations and their applications
-
Faculty of Science, Department of Applied Science
- Associate professor
- Takafumi NIIHARA
- Research Field
Meteoritics, Mineralogy, Petrology, Cosmochemistry
- Keyword(s)
Solar System, Meteorites, Astrobiology, Shock metamorphism
- Research theme
-
- Evolution of the early Solar System
- Rock-Water interaction on Mars
- Impact history of the Solar System
Outline of research activities


The aim of the research is to clarify the origin and evolution of the Solar System using various types of meteorite samples. Analytical techniques I am using for the studies are optical microscope, scanning electron microscope, electron probe micro analyzer (EPMA) and Micro Raman spectroscopy etc. Our target bodies are all of the celestial bodies include Earth. I am also joining the deep space exploration. My E/PO activities are exhibitions of meteorites and public lectures.
- Desired cooperation
-
- Micro analyses for rock and minerals
- Astromaterials researches
- Exhibition and public lecture
-
Faculty of Science, Department of Applied Science
- Lecturer
- Youichi YAMAZAKI
- Research Field
Functional Analysis, Probability Theory, Integral Theory
- Keyword(s)
Probability, Integral, FunctionSpace, Limit
- Research theme
-
- Properties of integrals
- The relation of the meaning of probability and mathematical probability theory
- Limit theorem of various functions and stochastic fluctuations
Outline of research activities

The integral of a function is intuitively the “area under the graph”, but it is now generalized in many ways. And when functions “converge” the function in some sense, do their integrals also converge it? The question “is this true?” can be a yes or no. The answer depends on the situation. By clarifying the nature of the concept of integrals, I am trying to clarify the mechanism by which such things do or do not happen.
Also, probability and integration are closely related. The so-called “expected value” or “variance (standard deviation)” is the integral of a random variable, and stochastic integrals are used to analyze stochastically varying processes such as stock prices.
However, the concept of “probability” that currently prevails in mathematics does not match well enough the image that people have of “probability. For this reason, there is still a debate among philosophers as to what probability is. This also has a negative impact on probability in school education. By resolving this issue, the human way of thinking about probability should evolve.- Desired cooperation
-
- Probability debate
- Research on integrals
-
Faculty of Science, Department of Physics
- Associate professor
- Keiko NAGAO
- Research Field
Particle Physics, Particle Cosmology
- Keyword(s)
Particle Physics, Dark Matter, Neutrino
- Research theme
-
- Particle Physics, Particle Cosmology
- Dark Matter
- Neutrino
Outline of research activities
Weakly interacting massive particles (WIMPs) are promising candidate for dark matter. Direct detection experiments of dark matter aim to detect nuclear recoil emitted by scattering of WIMPs and standard model particles. In directional dark matter detection, not only recoil energy but also direction of nuclear recoil are expected to be detected. It has the potential to give constraints on dark matter nature such as velocity distribution model. I theoretically study the possibility of the directional dark matter detection. My another interest is neutrino physics. Neutrino would be a hint to the Physics beyond the Standard Model as well as dark matter. I have constructed new theoretical models including both dark matter and neutrinos.
- Desired cooperation
-
- Particle Physics, Particle Cosmology
- Dark Matter
- Neutrino
-
Faculty of Science, Department of Physics
- Associate professor
- Makoto WATANABE
- Research Field
Optical and Infrared Astronomy, Astronomical Instrumentation
- Keyword(s)
Astronomy, Imaging, Spectroscopy, Polarimetry, Adaptive Optics, Wavefront Sensing, Active Galactic Nuclei
- Research theme
-
- Adaptive optics and its applications
- Internal structure, formation, and evolution of active galactic nuclei, and the interaction with host galaxy
Outline of research activities

The spatial resolution of images observed by the ground-based astronomical telescope is limited because of the wavefront distortion suffered by the turbulence of the earth atmosphere. In order to overcome this problem, we are studying the adaptive optics and developing the astronomical instruments with adaptive optics, which corrects the wavefront distortion in real-time. The applications of this technology into biological and medical fields are also being studied.
In addition, we are studying the internal structure, physical condition, formation, and evolution of the active galactic nuclei, which are active objects emitting a huge energy from the very compact region by mass accretion into the super-massive black hole at the center of galaxy, observing them with time-variability monitoring, polarimetry, and adaptive optics.
- Desired cooperation
-
- Development of the telescopes, microscopes, and measuring instruments with adaptive optics
-
Faculty of Science, Department of Physics
- Lecturer
- Daisuke YAMAUCHI
- Research Field
Cosmology, Gravity theory
- Keyword(s)
Inflation, Dark Energy, Dark Ages
- Research theme
-
- Accelerated expansion of the Universe from a modification of general relativity
- Dark Universe explored by radio telescopes
Outline of research activities

The latest cosmological observations strongly suggest the surprising fact that the Universe is undergoing an accelerated expansion at two very different times, immediately after the birth of the Universe and at the present time. However, this fact is incompatible with the property that gravity is an attractive force. An interesting fact is that the latest observational results suggest that a modification of general relativity may be manifested in the very early and current Universe. I believe that the key to the search for essentially new observables is to observe the “Dark Ages” and “Cosmic Dawn”, in which information about the very early Universe is preserved. Through radio observations that can probe these epochs, I aim to unravel the detailed history of the Universe.

- Desired cooperation
-
- Studies on an accelerated expansion of the Universe in the context of modified theory of gravity
- Studies on cosmology with radio observations
-
Faculty of Science, Department of Physics
- Lecturer
- Tetsuro KUBO
- Research Field
Condensed matter physics, Magnetism, Strongly-correlated electron systems, Toporogical materials
- Keyword(s)
Nuclear magnetic resonance (NMR) spectroscopy, f-electron systems, Weyl semimetals
- Research theme
-
- NMR study of strongly-correlated electron systems and toporogical materials
Outline of research activities


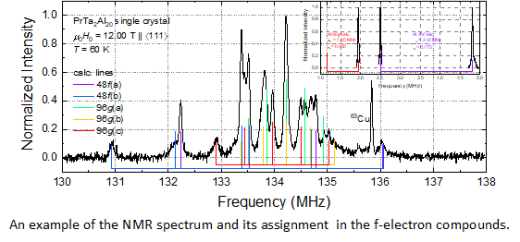
Our research interests span various quantum phenomena such as magnetism, superconductivity, and multipolar ordering in strongly-correlated electron systems, as well as Weyl fermion excitations in what are known as topological Weyl semimetals. The nuclear magnetic resonance (NMR) techniques we use are advantageous because they allow us to investigate microscopic electronic states on the laboratory scale.
We also have a keen interest in developing a mobile and easily reproducible NMR spectrometer by leveraging the latest radio frequency technologies.
- Desired cooperation
-
- Research in condensed matter physics using NMR techniques
- Development of mobile NMR spectrometers
-
Faculty of Science, Department of Zoology
- Professor
- Takahiro MURAKAMI
- Research Field
Evolutionary ecology, behavioral ecology
- Keyword(s)
Leaf-cutting ants, acoustic communication, anatomy, evolution, ecology, behavior
- Research theme
-
- Evolution of acoustic communication in ants
- Pest control and management of invasive alien species, such as fire ants
- FISH mapping of regeneration-related genes in amphibians and planarians
- A new fabric material development using ants and silkworms
Outline of research activities




The final goal of our research is to converse with ants. Ants have long been thought to engage in detailed communication using chemical substances such as pheromones. However, our researchis revealing that acoustic signals are also important toos of communication.We conducte detailed analyses of organs such as “ears” and “sound-producing organs”. It will be able to control the behavior of ants like leaf-cutting ants, which are significant damage against human society.
We have been collaborating with various stakeholders such as the Fukuoka City, Fukuoka Prefecture, and the Ministry of the Environment to control invasive alien ant species such as the red imported fire ant, the yellow crazy ant, and Argentine ant. In Okayama Prefcture, there have been reported of the little fire ant (Wasmannia auropunctata) at Mizushima Port, and we will continue to control and manage these ants.
By using silk produced by silworms, which domesticated in China 6,000 years ago, and the silks spun by black Japanese weaver ant in Okinawa, we conduct research to create new fabric sheets. We hope that as this research progresses, the black Japanese weaver ant can be a symbolic relationship with humans as the fourth demesticated insect.
- Desired cooperation
-
- Control and management of invasive alien ants
- Behavioral research of ants and other insects
- Development of communication device with ants using acoustic signals
- Domestication research of the black Japanese weaver ants
-
Faculty of Science, Department of Zoology
- Professor
- Yuji TAKENOSHITA
- Research Field
Primatology, Anthropology, Zoo Sciences, Socio-Ecology, Conservation Ecology, African Studies
- Keyword(s)
Primates, Gorilla, Zoo, Biodiversity Conservation, Africa, Human Evolution
- Research theme
-
- Studies on feeding ecology and life history strategies in wild western lowland gorilla (Gorilla g. gorilla)
- Cooperative breeding among primates
- Evolution of non-reproductive aspect of primate and human sexuality
Outline of research activities




Primates (precisely non-human primates), are the animal group that shares the most similarities with humans. They show high levels of intelligence and social skills. Additionally, many primate species live in tropical and subtropical regions and are considered keystone species that play a fundamental role in maintaining tropical ecosystems. Researching the society and ecology of primates can provide us with valuable insights into the evolution and nature of humans. This knowledge can help us better understand ourselves, as well as contribute to the conservation of biodiversity and the resolution of global environmental issues. My work involves studying the society and ecology of primates and other large and medium-sized mammals, mainly through field observations. I also examine human society from a zoological perspective and its evolution. Currently, my team and I are conducting long-term field research and conservation activities to protect wild gorillas in the tropical forests of Central Africa. We also conduct educational and animal welbeing activities in zoos and perform behavior observation research on Japanese macaques in Japan.
- Desired cooperation
-
- Development of ecological and behavioral data collection equipment and systems in tropical forests using ICT technology
- Practice of local ecosystem conservation activities through collaboration between researchers and citizens ( local community members)
- Zoo-based biodiversity conservation education activities
-
Faculty of Engineering, Department of Architecture
- Professor
- Fuminori HIRAYAMA
- Research Field
Architectural Design
- Keyword(s)
user participation design, user evaluation,workshop, public cultural facilities
- Research theme
-
- User Evaluation of Public Cultural Facilities
- Analysis of user opinions and verification of effectiveness of user participation design
- Functional changes in public cultural facilities
Outline of research activities





In the design of public cultural facilities, there are an increasing number of examples of design methods that incorporate the users’ ideas at the architectural design stage in order to promote active use.
Our laboratory has collected 70 cases of participatory design from all over Japan. The following participatory design practices were implemented in our laboratory, and the effectiveness of participatory design was verified through analysis of user opinions and post-completion evaluations of these practices.
・Kudamatsu City Community Exchange Center (2013)
・Okayama Prefectural Doctor’s Hall (2015)
・Sanagouchi Village Office (2017)
・Kashiwa City Southern Neighborhood Center (2018)
- Desired cooperation
-
- Public facility planning and design
- User-participatory design practices
- User evaluation analysis of public facilities




