-
理学部 応用数学科
- 教授
黒 木 慎 太 郎
- 研究分野
変換群論、トーリックトポロジー
- キーワード
群作用、(同変)コホモロジー、グラフ
- 研 究
テーマ -
- コホモロジー剛性問題
- GKM理論の幾何への応用
- 群作用を持つ空間の分類問題 など
研究活動の概要

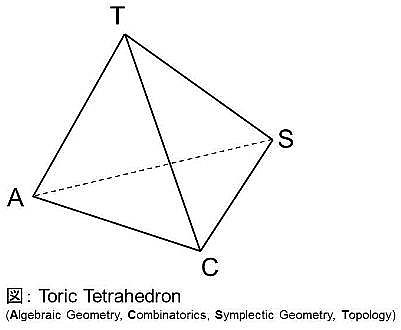
空間がある種の対称性を持つ場合を、群作用を持つ空間または空間上に群の作用があると言います。近年になって、トーリック多様体に代表されるトーラス作用を持つような空間を組み合わせ論的な道具を用いて調べる手法が開発されてきました(トーリックトポロジーと呼ばれています)。トーリックトポロジーは、幾何、代数、組み合わせ論という一見異なる3つの分野が交錯する分野と考えることができます。今後は、これら3つの分野がより強く結びついた空間を模索しながら、それらの間の関係をより深く理解し、最終的には未解決な問題の解決に挑戦したいと考えています。
- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 准教授
須 藤 清 一
- 研究分野
表現論、研究教育支援情報システム
- キーワード
リー群、リー環、ネットワーク、仮想化
- 研 究
テーマ -
- リー群およびリー環の構造とその表現
- 仮想化とネットワー ク を利用した安全かつ柔軟な研究・教育支援情報システムの構築と運用 など
研究活動の概要
主に無限次元のLie環とそれに付随するLie群の実現とその表現について研究する。
研究・教育支援情報システムに仮想化とネットワークを利用することで、多くの分野に対応し、かつ安全に運用可能な環境を開発する。研究・教育支援情報システムに仮想化とネットワークを利用することで、多くの分野に対応し、かつ安全に運用可能な支援環境を開発する。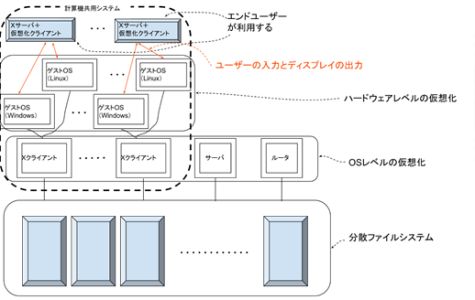
- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 講師
柴 田 大 樹
- 研究分野
代数群及びリー代数、表現論
- キーワード
ホップ代数、スーパー代数群、リー代数、モジュラー表現、超対称性
- 研 究
テーマ -
- スーパー群論へのホップ代数的アプローチ
- スーパー数学の非スーパー数学への応用
- モジュラー表現論
研究活動の概要
物理学からもたらされた概念である「超(スーパー)対称性」を数学の立場で研究しています。代数群 G は一般に複雑に”捻じれて”おりその性質を直接調べることは難しいですが、その”接平面”はリー代数 Lie(G) をなし、基礎体の標数がゼロの場合は G の性質をよく反映することが知られています。しかし正標数の場合状況は変わって、Lie(G) の代わりにハイパー代数と呼ばれるある種のホップ代数 hy(G) を用いる必要があります。
代数群、リー代数のスーパー類似物としてスーパー代数群、スーパー・リー代数と呼ばれるものが知られていますが、本研究ではこれまで上記の事実がスーパーの世界でも同様に成立することを示し、さらにその表現論にもホップ代数的アプローチが有効であることを実証してきました。今後はこれまで得られた結果を具体的なスーパー代数群に応用することで、モジュラー表現論を中心に非スーパー数学への寄与を目標に研究しています。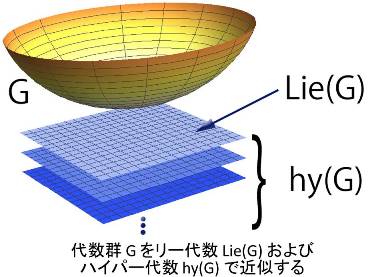
- 希望する
連携内容 -
- 理論物理学(超対称性理論、共形場理論など)への応用
-
理学部 基礎理学科
- 教授
伊 代 野 淳
- 研究分野
素粒子天文学
- キーワード
高エネルギー宇宙線、高エネルギー宇宙物理
- 研 究
テーマ -
- 高エネルギー宇宙線原子核の組成の研究
- ガンマ線天体の研究
- 流星・火球の研究
研究活動の概要

高エネルギー宇宙線の起源、加速メカニズム並びに伝播の謎を解き明かすために、宇宙線空気のシャワー観測実験によるデータ収集を行い、理論モデルに基づくシミュレーション結果との比較考察を行っています。また、太陽活動による宇宙線の影響についてモニタリング観測を行っています。研究方法としては、本学校内並びに全国の共同研究機関に設置した宇宙線空気シャワー観測装置によって、宇宙線の到来時間、到来方向とシャワーサイズのデータを蓄積することで行っています。
また近年は気球搭載型原子核乾板ガンマ線望遠鏡を用いた高エネルギーγ線天体現象の研究並びに、HIMAC重粒子ビームを用いた宇宙線原子核同定のための低感度化原子核乾板の開発と、それによる宇宙線重原子核組成の研究を行っています。2015年、2018年にはオーストラリアでの気球実験に成功し、データ解析を行っている。また、2022年にスケールを一桁大きくした気球実験を計画している。
- 希望する
連携内容 -
- 放射線測定器の開発
- 原子核乳剤の開発
- 原子核同定のための固体飛跡検出器の開発
-
理学部 基礎理学科
- 教授
森 嘉 久
- 研究分野
高圧科学、放射光実験
- キーワード
高圧、熱電素子、半導体、X線、放射光
- 研 究
テーマ -
- シリサイド系熱電素子の高圧合成
- 放射光を利用した高圧構造実験
- 種子や卵の圧力耐性研究
- 測定系における通信制御プログラムの開発 など
研究活動の概要

高圧力の技術を活用して、基礎研究から応用研究まで幅広く研究しています。
研究対象は、半導体物質のようなハードマテリアルから植物の種子などのソフトマテリアルまで様々。測定装置や治具なども自分達で設計、製作するなど常に考える研究を遂行しています。
- 希望する
連携内容 -
- 圧力印加による物性変化に関する分野
- 圧力下での構造・物性変化に関する分野
-
理学部 物理学科
- 准教授
長 尾 桂 子
- 研究分野
素粒子物理学、素粒子論的宇宙論
- キーワード
素粒子、宇宙、暗黒物質、ニュートリノ
- 研 究
テーマ -
- 素粒子論・素粒子論的宇宙論
- 宇宙の暗黒物質
- ニュートリノ など
研究活動の概要
物質を小さく分解していくと、すべては素粒子と呼ばれるそれ以上分解できない粒子に分けることができると考えられています。現在知られている素粒子の枠組みは実験と非常によく合う成功した理論ですが、一方でそれだけでは説明できないことがいくつも存在しています。その1つが宇宙に存在する暗黒物質です。暗黒物質は我々の知っている物質の約5倍のエネルギー密度を宇宙で占めており、これまでにわかっている素粒子の枠組みで説明することはできません。そこで、暗黒物質を調べることによって、素粒子や宇宙についてもっと本質的なことがわかると期待されています。私は、実験で暗黒物質の性質を解明する方法や、そこからわかる素粒子の性質について研究しています。また、素粒子の1種類であるニュートリノも、その質量については未知の部分が多く、暗黒物質とともに、新しい素粒子理論へのヒントであると考えられています。暗黒物質とニュートリノの性質を理論面から調べることによって、宇宙と素粒子の2つの領域にわたる物質の謎に迫ります。
- 希望する
連携内容 -
- 素粒子論に関する研究
- 初期宇宙についての研究
- 物理教育 など
-
理学部 動物学科
- 教授
村 上 貴 弘
- 研究分野
進化生態学、動物行動学
- キーワード
ハキリアリ、音声コミュニケーション、解剖、進化、生態、行動
- 研 究
テーマ -
- ハキリアリの音声コミュニケーションの進化
- ヒアリなどの侵略的外来生物の防除研究
- クロトゲアリとカイコによる新規生地シートの生成
研究活動の概要




アリと会話をする。これが研究の最終的なゴールです。アリは、フェロモンなどの化学物質を用いて詳細なコミュニケーションを行っているものと考えられてきました。しかしながら、発音器官をこすり合わせることによって発する振動音も、コミュニケーションの重要なツールであることが我々の研究から明らかになりつつあります。音声解析や操作実験、そして解剖学的手法を用いた「耳」や「発音器官」の詳細な解析を行っています。この研究が進展することにより、ハキリアリのような甚大な被害を人間社会にもたらす昆虫の行動を制御することが可能になるものと考えています。
2017年に初めて日本国内に侵入が確認された侵略的外来生物のヒアリをはじめとした指定外来生物(アルゼンチンアリ、ハヤトゲフシアリ、アカカミアリ、コカミアリなど)の防除を福岡市、福岡県、環境省などさまざまなステークホルダーと協働して行ってきました。岡山県内では水島港でコカミアリの定着事例が報告されており、今後適切な防除・モニタリング作業を進めていきます。
再生能力の高いイモリやプラナリアを用いた再生関連遺伝子の染色体上へのFIAHマッピングを行ってきた。また再生能力の指標であるテロメア領域のマッピングも昆虫を含めて幅広く行っています。
沖縄に生息する、幼虫の出す糸で巣を紡ぐクロとげアリと6,000年前に中国で家畜化されたカイコの出す絹糸を用いることにより、新規の生地シートを作成する研究をしています。この研究が発展すると第4の家畜化された昆虫としてクロトゲアリが人間と共生関係を結べるものと期待しています。- 希望する
連携内容 -
- 防虫・外来生物防除
- アリなどの昆虫の行動研究
- アリと会話をする機械の開発
- クロトゲアリの家畜化研究
-
工学部 情報工学科
- 准教授
尾 崎 亮
- 研究分野
計算機システム、教育工学
- キーワード
FPGA、複合クラスタ、機械学習
- 研 究
テーマ -
- PC-FPGA複合クラスタ
- 学習効率の良い独習用eラーニングシステム
- デザイン教育 など
研究活動の概要

複合クラスタという高性能コンピュータシステムを提案し、応用研究を行っています。コンピュータから家庭用電子機器を制御したり、逆に家庭用電子機器からコンピュータを制御したりといった、コンピュータと家庭用電子機器の協調動作を簡便に行うための共通の枠組みを提供します。また、教育工学分野では、学生の自習時間を増やすための取り組みや、講義内でのソフトウェアのチーム開発といった実践教育に取り組んでいます。

- 希望する
連携内容 -
- PC-FPGA複合クラスタに関する応用事例
- ソフトウェア開発モデルに関する実践教育
-
工学部 建築学科
- 教授
中 西 啓 二
- 研究分野
建築耐震構造,耐震診断
- キーワード
RC構造,鉄骨構造,免制振構造,耐震診断
- 研 究
テーマ -
- 鉄骨立体トラスの接合部耐力に関する研究
- 面格子壁,合板耐震補強壁の耐力に関する研究
- 免震・制振構造を用いた耐震補強に関する研究
- 露出型柱脚に関する研究など
研究活動の概要



建築耐震構造を専門としており、実験で部材の破壊モードや耐力を理解した上で、解析により実験を再現し、それらの結果を元に設計法を確立するという流れで研究を行っております。
2015年に本学に着任してからは、地元企業との連携で鋼管を用いたトラス構造の研究や、面格子壁の研究を行っております。さらに2016年度からは、小型振動台を用いて、免震・制振構造の研究にも着手しました。
2020年からは、災害後に避難所となる体育館の耐震補強、制震補強に関する実験および解析研究を行っております。
今後は、熊本地震などのような近い将来予想されている巨大地震に対して被害を最小にするための構造に関する研究を、地元企業との連携も含めて進めていく予定です。
- 希望する
連携内容 -
- 鉄骨造,RC造,RCS造などの実験及び解析的研究
- 免震,制振構造を用いた耐震補強に関する研究
- 最適設計に関する研究 など
-
工学部 建築学科
- 教授
平 山 文 則
- 研究分野
建築設計
- キーワード
利用者参加型設計、ワークショップ、利用者評価、公共文化施設
- 研 究
テーマ -
- 公共施設の利用者評価
- 利用者参加型設計の利用者意見分析及び効果の検証
- 美術館、博物館、図書館等公共文化施設の機能変化 など
研究活動の概要





●公共文化施設設計においては、活発な利用を促進することを目的に、建築設計段階に利用者の考えを取り入れた設計手法(利用者参加型設計)を採用する事例が増えている。
●当研究室では、全国の参加型設計事例を70事例程度収集するとともに、研究室でも参加型設計を実践し(2013年度:下松市地域交流拠点、2015年度:岡山県医師会館、2017年度:佐那河内村役場、2018年度:柏市南部近隣センター)、それらの利用者意見分析及び竣工後評価から、参加型設計の効果を検証する。
- 希望する
連携内容 -
- 公共施設の企画・設計
- ワークショップ、利用者参加型設計の実践
- 公共施設の利用者評価分析 など
-
工学部 建築学科
- 准教授
馬 淵 大 宇
- 研究分野
建築計画学、建築設計方法論、建築設計
- キーワード
Virtual Reality、心理・生理計測、被験者実験
- 研 究
テーマ -
- 設計者とユーザーがコ・クリエーション(協働創作)する手法の研究
- ストレス指標を基にユーザーの視点を創作に反映する手法の開発
- VRを用いてユーザーの空間認識をトレーニングする手法の開発
- VRを用いてアルゴリズムデザインを協働創作する手法の開発など
研究活動の概要


今日、「ものづくり」のあり方は、大きな変革を迎えています。その変革の1つにコ・クリエーション(協働創作)があり、作り手と使い手の隔たりを超えた、新しい「ものづくり」のあり方が模索されています。当研究室では、心理・生理計測(ストレス指標)やVirtual Reality(VR)等を用いて作り手と使い手の垣根を可能な限り取り払い、コ・クリエーション可能な場の構築を目指しています。

- 希望する
連携内容 -
- ストレス指標やVRを用いた「ものづくり」の円滑化手法の実践
- 内外装デザインの共同開発
- 中・小規模な建築物の設計
-
情報理工学部 情報理工学科
- 教授
赤 木 徹 也
- 研究分野
メカトロニクス,空気圧制御機器,機械制御工学
- キーワード
ソフトアクチュエータ,ウェアラブル制御機器,組込みコントローラ
- 研 究
テーマ -
- 低価格柔軟空気圧アクチュエータの開発と在宅リハビリテーション機器への応用
- 低価格ウェアラブル流体制御弁の開発と応用
- 柔軟空気圧アクチュエータを用いた各種柔軟ロボットの開発
研究活動の概要




圧縮性による柔軟性を有し、軽量で力/質量比の高く、更に安価な空気圧ソフトアクチュエータの特徴を活かして、使い捨て可能なホームリハビリテーション機器の開発やその制御機器やロボットへの応用を行う。具体的には、曲がっても使える柔軟な空気圧シリンダを開発し、ポータブルリハビリテーション機器へ応用した。また、材料費が千円以下の安価な弁としてチューブの屈曲を利用したサーボ弁を開発した。また、変位センサ内蔵型ゴム人工筋の開発、伸長型柔軟アクチュエータを用いた配管検査ロボットの開発などの研究を行っている。さらに、人材のグローバル化をめざし、所属院生の全員が国際会議で講演発表を行っている。

- 希望する
連携内容 -
- 組込み技術を用いた空気圧駆動ウェアラブル制御機器の開発と応用
- 小型・軽量・低価格な空気圧制御弁の開発
- 柔軟アクチュエータや柔軟センサの開発と応用
-
情報理工学部 情報理工学科
- 教授
大 山 和 紀
- 研究分野
ゲーム工学
- キーワード
ゲームプログラミング、ゲームによる社会貢献
- 研 究
テーマ -
- リアルタイムレンダリング
- ゲームがもたらす行動変容 など
研究活動の概要

コンピューターゲームは様々な最先端を取り入れながら技術と共に成長してきました。その中でもインタラクティブ性や没入感を支えるリアルタイムレンダリング技術、他者との結びつきを支えるネットワークを中心に研究しています。ゲームにはまる仕組みやソーシャルメディアに関する研究などを通じて、ゲームによる社会貢献(教育や地域活性化、美観や広報活動など)や、ゲームが社会に果たす役割などについても取り組んでいきたいと考えています。

- 希望する
連携内容 -
- プログラミング教育、地域の情報教育サポート
- 高齢者向けゲーム、見守りシステム
- ゲームによる地域活性化、美観、広報活動 など
-
情報理工学部 情報理工学科
- 教授
河 野 敏 行
- 研究分野
数値解析、ICT活用教育
- キーワード
線型方程式、
- 研 究
テーマ -
- 線型方程式の解法アルゴリズムの改良
- 並列アルゴリズムの研究
- ICTを活用した遠隔講義の実施についての改善
- プログラミング学習をサポートするコンテンツの開発など
研究活動の概要

様々な現象を解析する際に、連立方程式を計算することが必要となり、解析全体の作業の中で最も計算時間のかかる部分である。現象をモデル化し、偏微分方程式を離散化した際に、そのような問題が得られる。これらの問題を高速に正確に解くことで、産業や技術の基盤を支えるものとなる。研究ではアルゴリズムの違いによる計算過程の変化の比較、誤差のふるまいによるアルゴリズムの特性を解析する。
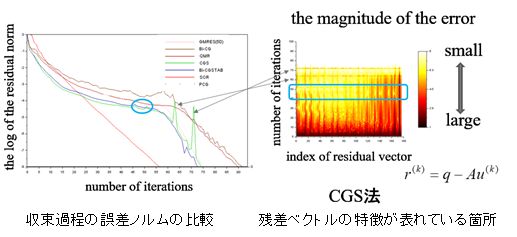
日本教育情報学会のICT活用研究会にて、ICTを活用した教育の情報共有を行っている。- 希望する
連携内容 -
- 線型方程式の解法
- ICTを活用した教育 など
-
情報理工学部 情報理工学科
- 教授
榊 原 道 夫
- 研究分野
数値解析、計算科学、応用数学
- キーワード
離散化手法、数理モデル、最適化手法
- 研 究
テーマ -
- 情報科学分野で用いられている手法(交互最小二乗法)の数理的研究。
- 微分の概念を拡張し、より複雑な対象に対する最適化手法の開発。
- 組込ソフトに使われる簡易関数(逆三角関数、ランバートW関数)計算法の研究。 など
研究活動の概要

観測されたデータから知りたい情報を推測する合理的な手法の開発は多くの応用分野が存在する。その手法の一つとして行列の分解を行う交互最小二乗法がある。この手法は心理学データの分析から画像処理に及ぶ広い分野で用いられている。しかし、この手法の理論的背景は十分に明らかにされているようではない。交互最小二乗法の理論的背景を明らかにする研究を中心に多様な興味の下研究を行っている。
- 希望する
連携内容 -
- 数理モデルの立てられていない問題全般。 など
-
情報理工学部 情報理工学科
- 教授
下 田 紀 之
- 研究分野
デジタルゲーム
- キーワード
ゲーム開発、ゲーム制作、ゲームメカニクス、プロジェクト管理
- 研 究
テーマ -
- デジタルゲーム制作
- ゲームメカニクス
- デジタルゲームの開発プロジェクト管理など
研究活動の概要
デジタルゲームは工業製品でありながらも一種の総合芸術作品でもあり、その企画開発には工学的な手法をそのまま適用できません。デジタルゲームの企画開発には創作的な魅力と工業的な品質を両立できるようなアプローチが求められます。そのためにはどのような制作を行わねばならないのか、どのようにプロジェクトを管理すべきかというテーマを研究しています。またゲームは一種のシステムであり、多数のシステムが複合することで一つのゲームシステムを成立させています。私はこのゲームメカニクスと呼ばれるシステムも研究しています。
- 希望する
連携内容 -
- eスポーツ研究
- バーチャルリアリティ研究
- ゲーミフィケーション研究など
-
情報理工学部 情報理工学科
- 教授
三 宅 新 二
- 研究分野
学習支援システム、ソフトウェア工学
- キーワード
学習支援システム、理解、気づき
- 研 究
テーマ -
- アルゴリズム、プログラミングの学習支援システムに関する研究
研究活動の概要
分かったつもりでも、異なる視点から見ると、不明点を確認できることがあります。
理解しづらい教材を少しでも取り組みやすくし、異なる視点での確認を促し、理解しやすい学習システムの構築を研究しています。
従来のCAI、eラーニングの手法をベースとして、アルゴリズム、プログラミング等における学習支援システムを構築し、公開することを目指しています。
また、簡単なパズル等の解法を提示するシステムにより、論理的に考える訓練ができることについても研究しています。- 希望する
連携内容 -
- アルゴリズム、プログラミングに関する教育サポート
-
生命科学部 生物科学科
- 准教授
田 所 竜 介
- 研究分野
細胞生物学、発生生物学、コスメトロジー
- キーワード
メラニン色素、オルガネラ、細胞間輸送、皮膚
- 研 究
テーマ -
- 体色形成時の色素輸送の機構解明
- 皮膚科学
- 化粧品開発への応用
研究活動の概要

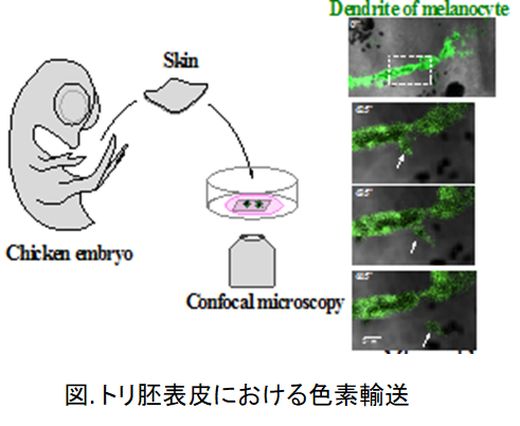
皮膚に存在するメラニン色素は紫外線から身を守るための防御壁となる一方、シミなど美容上の問題を引き起こす厄介者として嫌遠される。また、色素異常が社会生活上の心の負担を招くなど、色素は我々の生活の質と密接に関係している。メラニン色素は、体色が作られる過程において、表皮に存在する色素細胞(メラノサイト)において合成される。メラノサイト内にはメラニン産生に特化したメラノソームと呼ばれる細胞小器官があり、メラニンを含むメラノソームが隣接する表皮細胞へと輸送されることで表皮に沈着する。この細胞間輸送のメカニズムを理解することは、化粧品開発および生物学において極めて重要であるが、そのメカニズムの詳細は未だなお不明である。
私は、ニワトリ胚の表皮をモデルとして用い、実際の表皮内で起こる色素輸送を直接解析する手法を確立した。この手法を駆使して、色素輸送の全貌を明らかにする。
- 希望する
連携内容 -
- 化粧品開発
- 皮膚科学
- 発生生物学、再生工学、コンピューターシミュレーション
-
生命科学部 医療技術学科
- 教授
木 場 崇 剛
- 研究分野
消化器病学、臨床腫瘍学
- キーワード
消化管臓器、再生、増殖、発癌
- 研 究
テーマ -
- 消化管臓器における再生・増殖に関わる神経因子の役割の解明 など
研究活動の概要




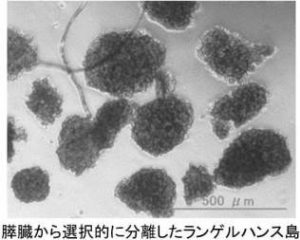
これまで消化器病専門医として各種消化器内視鏡検査並びにがん薬物療法専門医として各種癌腫の抗癌剤治療に関する臨床および研究に従事しておりました。また、膵B細胞の再生および増殖の神経因子の役割を研究テーマとしてきました。膵B細胞の増殖因子としては、多くの遺伝子の関与が指摘されていますが、神経因子が膵B細胞の増殖の影響を与えているという報告は、私の研究室以外には見当たりません。新たな視点から膵B細胞の再生および増殖に道を開き、糖尿病患者や膵臓癌患者に福音をもたらしたいと考えております。
- 希望する
連携内容 -
- 消化管臓器の再生・増殖に関わる臨床応用に向けた各種研究開発 など
-
生命科学部 医療技術学科
- 教授
堀 純 也
- 研究分野
臨床工学,電気医療機器の安全管理,医学教育
- キーワード
除細動器,AED,電気メス,血液浄化療法,BLS
- 研 究
テーマ -
- 除細動器,電気メスなどの高エネルギーデバイスの安全性評価
- 血液浄化に関する各種センサ開発
- 医学教育用の各種教育ツールの開発 など
研究活動の概要

(1)医療の現場では除細動器やAED、電気メスといった電気を利用した医療機器が数多く使われています。これらの機器は適切に使用されなければ感電や熱傷事故の原因となります。そこで、本研究では不適切な使用をした場合にどのような電気的危険があるかについて調べています。
(2)血液浄化療法においては非侵襲的に患者様の情報を得ることが重要となります。化学発光を利用した尿素センサなどのセンサ開発・改良を行っています。
(3)臨床工学技士の養成を行う上では、様々な実習を行う必要がありますが、実際の患者様を相手にするわけにはいきません。そこで、生体の代わりになるような実習用教育教材の開発を行っています。また、一般市民向けの一次救命講習会などで利用できる教育ツールの開発も行っています。

- 希望する
連携内容 -
- 医療機器の安全評価デバイスの開発
- 医学教育に関する教育教材開発 など








