-
理学部 応用数学科
- 教授
青 山 崇 洋
- 研究分野
高次元測度論、確率論、解析的整数論
- キーワード
高次元離散分布、多重ゼータ関数
- 研 究
テーマ -
- 多重ゼータ関数を用いた高次元離散型測度論
- グラフ上のランダムウォーク
- 確率過程論 など
研究活動の概要高次元離散型測度の研究は1次元の離散型、連続型並びに高次元離散型と比較すると数学的に使える情報が乏しい。これらの問題を解決するため、新たな多重ゼータ関数を導入することにより多くの高次元離散型測度が記述可能であることを確認してきた。特に無限個の点に重みを持つ高次元離散型測度論に関する数学的理論の発展を目指している。グラフ上のランダムウォーク等をはじめとする確率論等への応用にも興味を持って取り組んでいます。
- 希望する
連携内容 -
- データサイエンス
- 機械学習
- 数理ファイナンス など
-
理学部 応用数学科
- 教授
大 江 貴 司
- 研究分野
偏微分方程式の逆問題の数値解析的研究
- キーワード
偏微分方程式、逆問題、数値解析
- 研 究
テーマ -
- 波動方程式における波源再構成問題の数値解析
- 逆散乱問題における介在物再構成問題の数値解析
- 異常拡散現象の数値解析
- 計算が不安定になる問題に対する安定な解法の開発
研究活動の概要
偏微分方程式の逆問題とは、大まかにいえば、直接には触れることのできないものを、外部にある情報から推定する問題です。例えばX線CTやソーナーなどを考えていただき、それらの数学的な表現であると考えていただければよろしいかと思います。
私の研究室では、偏微分方程式の逆問題に対する、簡便で、精度の高い数値解析手法の研究と開発を行っています。特に騒音や探知の難しい音源について、その位置や動きを推定する手法に関する研究を進めています。
また、土壌の中の汚染物質の広がりの時間変化を追跡する異常拡散方程式について、数値解析手法の開発を行っています。
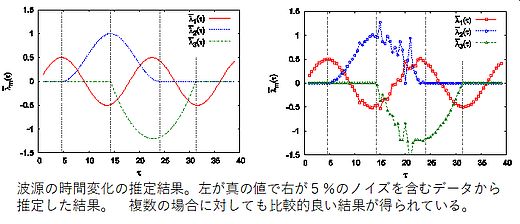
- 希望する
連携内容 -
- 音源や汚染源の位置や動きを推定する方法に関する数理解析
- 土壌の中の汚染物質の広がりの数理解析に関する研究
-
理学部 応用数学科
- 教授
黒 木 慎 太 郎
- 研究分野
変換群論、トーリックトポロジー
- キーワード
群作用、(同変)コホモロジー、グラフ
- 研 究
テーマ -
- コホモロジー剛性問題
- GKM理論の幾何への応用
- 群作用を持つ空間の分類問題 など
研究活動の概要

空間がある種の対称性を持つ場合を、群作用を持つ空間または空間上に群の作用があると言います。近年になって、トーリック多様体に代表されるトーラス作用を持つような空間を組み合わせ論的な道具を用いて調べる手法が開発されてきました(トーリックトポロジーと呼ばれています)。トーリックトポロジーは、幾何、代数、組み合わせ論という一見異なる3つの分野が交錯する分野と考えることができます。今後は、これら3つの分野がより強く結びついた空間を模索しながら、それらの間の関係をより深く理解し、最終的には未解決な問題の解決に挑戦したいと考えています。
- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 教授
浜 畑 芳 紀
- 研究分野
代数学、数論
- キーワード
デデキント和、ゼータ関数、ディリクレ級数、保型形式、関数体
- 研 究
テーマ -
- 正標数のデデキント和の研究
- ゼータ関数、L関数、ディリクレ級数の特殊値の研究
- 関数体の数論 など
研究活動の概要
代数体と有限体上の1変数代数関数体の類似性は古くから知られています。数論はこの両方の土台の上で相互に影響しながら発展しました。私は、デデキント和という特別な数を利用して、数論に生息する関数たち、たとえば、ゼータ関数、L関数、ディリクレ級数、保型形式、保型関数などの性質を研究しています。また、このような関数を利用して、数の性質を研究しています。
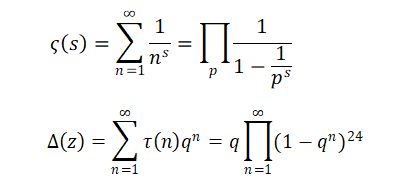
- 希望する
連携内容 -
- 有限体の研究 など
-
理学部 応用数学科
- 教授
坂 内 真 三
- 研究分野
代数幾何学
- キーワード
代数曲面、代数曲線、ガロア分岐被覆、グレブナー基底
- 研 究
テーマ -
- 平面曲線の埋め込み位相の分類
- 幾何学的ガロアの逆問題やガロア分岐被覆の応用
- 代数幾何学の計算的側面 など
研究活動の概要「代数幾何学」は多項式で定義された図形の性質を研究する分野です。 多項式で定義されている故に、 代数の理論を使って、 図形の幾何学的な性質を調べることができます。
私は代数幾何学の中でも主に代数曲線や代数曲面という次元が低い図形を研究対象にしています。 一見似ている曲線をどの様に区別するかの「不変量」を考えたり、 与えられた条件を満たす曲線が存在するか否かの「存在問題」、 存在するとして、 具体的に書き下す「構成問題」に興味を持って研究をしています。 具体的な多項式を扱うことも多いので、コンピュータを使って計算をすることもあります。

- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 教授
渡 邊 道 之
- 研究分野
数学、解析学、数理物理学
- キーワード
偏微分方程式論、散乱理論、逆問題
- 研 究
テーマ -
- 偏微分方程式の解の一部の情報から方程式の未知係数を逆算する研究
- 非線形波動と量子力学における基礎方程式との関連性
- 量子力学の散乱理論と地震波の弾性波動方程式の関連性 など
研究活動の概要



逆問題は、観測された現象や結果から直接的には観測できない原因や未知の物理的特性を推定する問題です。例えば、地震波のデータから地下構造や地震源の特性を推定する問題や、散乱粒子の振る舞いから原子や分子の配列構造に依存するポテンシャルを決定する問題が逆問題の例です。
これらの問題は、偏微分方程式を用いて数学的に定式化することができます。未知の物理的特性は、方程式の係数などで表現されます。逆問題の数学的解析では、方程式の解の部分的情報から方程式の未知の係数などを逆算する手法を開発し、その手法の解析的性質を調べることが課題となります。
本研究室では、量子力学における散乱の逆問題と非線形波動との関連性、さらに量子力学の散乱理論と地震波の弾性方程式との関連性について研究しています。散乱理論は、入射波が物体やポテンシャルによって散乱され、散乱波が生成される現象を記述する数学的な枠組みです。一方、地震波の弾性波動方程式は、地震や地下の構造物によって散乱される波動現象を記述します。これらの現象は、数学的には類似しているため、散乱理論の手法を地震波の研究に応用することができます。このような研究が進むことで、地震波の解析や予測が向上し、地球の内部構造の解明や地下資源の探索、津波の被害制御などの応用が可能になります。
数学的手法や解析を通じて、量子力学の散乱や非線形波動、地震波などの異なる現象間の関連性を明らかにすることは、新たな知見をもたらし、応用分野においても有益な成果を生むことが期待されます。異なる分野や現象の間に存在する数学的なつながりを見出し、その理解を深めることは数学研究の魅力でもあります。- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 准教授
阿 部 拓
- 研究分野
幾何学,トポロジー,変換群
- キーワード
代数多様体,群の作用,コホモロジー環
- 研 究
テーマ -
- 群作用を持つ代数多様体のトポロジー
- ヘッセンバーグ多様体
- 旗多様体,トーリック多様体
研究活動の概要私は「対称性を持つ空間」という言葉をキーワードに数学の研究をしています。その中でも、代数・幾何・組み合わせ論といった複数の分野が交わる数学に特に関心を持っています。
このような分野で数学を展開することの魅力は、一つの現象がいくつもの解釈を持ち得るというところにあります。一方では幾何的な解釈があり、他方では表現論的な解釈が、また他方では組み合わせ論的な解釈があるということが折に触れて現れ、数学の豊かさに触れることができます。特に、空間が持つ幾何学的ないしトポロジー的な量を、代数や組合せ論の言葉で具体的に理解できたときの面白さは格別です。最近はヘッセンバーグ多様体と呼ばれる空間の幾何学とトポロジーに興味を持って研究しています。
- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 准教授
瓜 屋 航 太
- 研究分野
偏微分方程式論
- キーワード
非線形分散型方程式、 調和解析、 フーリエ解析
- 研 究
テーマ -
- 非線形シュレディンガー方程式系の解の長時間挙動
- 非線形シュレディンガー方程式系の初期値問題の可解性
- 調和解析による不等式の研究
研究活動の概要代表的な非線形分散型方程式である非線形シュレディンガー方程式およびその連立系に対して、 初期値問題の可解性、 解の長時間挙動、 解の有限時間爆発などを調和解析、 関数解析的手法により研究している。 現在の研究では、 方程式に現れる分散係数や消散項の係数に応じて解の挙動がどのように変化するかについて興味があります。純粋に数学的問題意識から研究に取り組んでいますが、 物理的な実在と関連した研究を行うことも一つの目標です。
非線形分散型方程式にはソリトンと呼ばれる空間的な形状を保ったまま伝播する解の存在が知られており、 津波はそのような解に対応する現象と言われています。数学的には方程式がもつ分散性と非線形性のバランスがつり合っている状態と解釈することができます。
- 希望する
連携内容 -
- 非線形光学等に現れる数理モデル
-
理学部 応用数学科
- 准教授
鬼 塚 政 一
- 研究分野
常微分方程式の安定性
- キーワード
常微分方程式、定性的理論、安定性
- 研 究
テーマ -
- 非自励システムの指数安定性
- 非自励システムの安定性と有界性に関する同値条件
- 解空間に同次性を有する常微分方程式のリヤプノフ安定性
研究活動の概要


常微分方程式の定性的理論における基礎的な研究を行う。本研究では、対象とする非自励システム(常微分方程式系)の全ての解に着目し、システムに現れる係数(変数係数)が解の振る舞いにどのような影響を与えているかについて考察する。特に、リヤプノフの安定性、一様安定性、吸収性、一様吸収性、漸近安定性、一様漸近安定性、指数安定性の分類に焦点を当て、ラグランジュ安定性(有界性)との関連性も明らかにする。これらの本質を見抜き理解することで、常微分方程式の発展に寄与することを目的としたい。
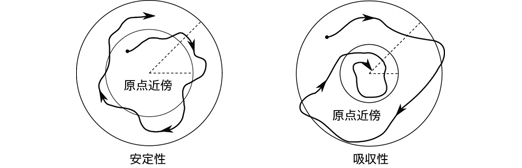
また、種々の研究領域に現れる常微分方程式、例えば、制御系や生態モデルに対して、得られた理論を応用し、新たな研究分野の開拓に挑戦する。- 希望する
連携内容 -
- ロバスト制御
-
理学部 応用数学科
- 准教授
須 藤 清 一
- 研究分野
表現論、研究教育支援情報システム
- キーワード
リー群、リー環、ネットワーク、仮想化
- 研 究
テーマ -
- リー群およびリー環の構造とその表現
- 仮想化とネットワー ク を利用した安全かつ柔軟な研究・教育支援情報システムの構築と運用 など
研究活動の概要
主に無限次元のLie環とそれに付随するLie群の実現とその表現について研究する。
研究・教育支援情報システムに仮想化とネットワークを利用することで、多くの分野に対応し、かつ安全に運用可能な環境を開発する。研究・教育支援情報システムに仮想化とネットワークを利用することで、多くの分野に対応し、かつ安全に運用可能な支援環境を開発する。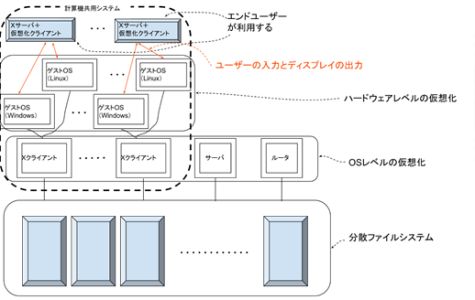
- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 准教授
森 義 之
- 研究分野
グラフ理論および有限群の表現論
- キーワード
グラフ理論、表現論、量子コンピューター
- 研 究
テーマ -
- 有限群とグラフ理論
- 結び目、絡み目
- 整数論とコンピューターを用いた計算
研究活動の概要有限群やグラフの構造や性質を解明する事、グラフの同形の判定。
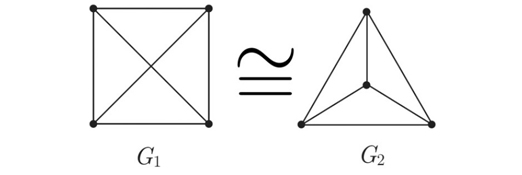
結び目、絡み目の多項式不変量の計算。
- 希望する
連携内容 -
- グラフ理論の応用
- 結び目、絡み目
-
理学部 応用数学科
- 准教授
山 田 紀 美 子
- 研究分野
代数幾何学におけるモジュライ空間
- キーワード
代数曲面上のベクトル束のモジュライ、特異点、小平次元
- 研 究
テーマ -
- 代数曲面上のベクトル束のモジュライ
- モジュライの特異点・局所定義式
- モジュライの小平次元 など
研究活動の概要
専門分野は、代数幾何学です。そこでは、多項式のゼロ点集合(代数多様体)を考えます。例えば、直線、円、双曲線、放物線が代数多様体となります。
ある一定の性質を持つ幾何的対象を全て集めてきた集合をモジュライ空間と呼びます。複素代数曲面X上の安定ベクトル束のモジュライ空間は、具体的な代数多様体の例として、活発に調べられています。
代数多様体Mに対しては、小平次元が定まります。Mの小平次元は、Mの曲率と関係する大事な不変量です。また、高次元多様体を理解するために極小モデル理論があります。これは、多様体を、その部分空間を爆発・つぶすことで手術して、より分かりやすいシンプルな多様体に変えるプログラムです。
私は、モジュライMの特異点、小平次元、極小モデルプログラムに興味があります。
(1)大きなクラスの代数曲面X上のベクトル束のモジュライ空間の極小モデル理論を、
モジュライの言葉を使って記述しました。
(2)モジュライMの特異点を調べ、下部曲面Xの構造が比較的平易な時に、特異点が
「たちがよい」ことを示しました。それを使い、Mの小平次元を計算しました。- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 講師
井 上 雅 照
- 研究分野
位相幾何学
- キーワード
ホモトピー論
- 研 究
テーマ -
- Hit problem について
研究活動の概要位数2の有限体上のn変数多項式環には、Steenrod代数が作用していて、この作用の極小な生成元を求める問題が Hit problem でございます。多項式環には、一般線型群も作用していて、互いの作用は可換でございます。代数のはなしのようにも見えますが、位相幾何学的な背景もあり、さまざまな観点から考察を進めております。
- 希望する
連携内容 -
- -
-
理学部 応用数学科
- 講師
陰 山 真 矢
- 研究分野
数理モデル、数値シミュレーション
- キーワード
偏微分方程式、反応拡散系、非線形現象、パターン形成
- 研 究
テーマ -
- 植生と気候のフィードバックモデルに対する研究
- 社会性昆虫の営巣メカニズムに関する研究 など
研究活動の概要


地球における植生と気候の相互作用システムを非常に単純化した仮想の惑星「デイジーワールド」には、白色と黒色のデイジーしか生息していません。2色のデイジーは互いの生育域を争いながら、惑星の温度を自分たちにとって快適であるように調節しています。このデイジーワールドの数理モデルに対して、数学解析と数値シミュレーションの両方面から研究し、モデル方程式の成り立ちや解の構造といった基礎的研究に限らず、デイジーワールドモデルを使って私たちが直面している社会問題を解決できないか、という応用化の可能性探求にも取り組んでいます。また、その他にも様々な非線形現象を記述する数理モデルに興味があり、社会に貢献できる研究を目指しています。

- 希望する
連携内容 -
- 衛星データ活用に関する研究
- 地球環境保全関連研究 など
-
理学部 応用数学科
- 講師
柴 田 大 樹
- 研究分野
代数群及びリー代数、表現論
- キーワード
ホップ代数、スーパー代数群、リー代数、モジュラー表現、超対称性
- 研 究
テーマ -
- スーパー群論へのホップ代数的アプローチ
- スーパー数学の非スーパー数学への応用
- モジュラー表現論
研究活動の概要
物理学からもたらされた概念である「超(スーパー)対称性」を数学の立場で研究しています。代数群 G は一般に複雑に”捻じれて”おりその性質を直接調べることは難しいですが、その”接平面”はリー代数 Lie(G) をなし、基礎体の標数がゼロの場合は G の性質をよく反映することが知られています。しかし正標数の場合状況は変わって、Lie(G) の代わりにハイパー代数と呼ばれるある種のホップ代数 hy(G) を用いる必要があります。
代数群、リー代数のスーパー類似物としてスーパー代数群、スーパー・リー代数と呼ばれるものが知られていますが、本研究ではこれまで上記の事実がスーパーの世界でも同様に成立することを示し、さらにその表現論にもホップ代数的アプローチが有効であることを実証してきました。今後はこれまで得られた結果を具体的なスーパー代数群に応用することで、モジュラー表現論を中心に非スーパー数学への寄与を目標に研究しています。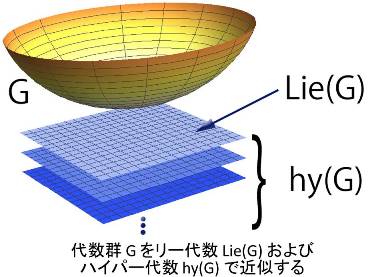
- 希望する
連携内容 -
- 理論物理学(超対称性理論、共形場理論など)への応用
-
理学部 基礎理学科
- 教授
荒 谷 督 司
- 研究分野
代数学
- キーワード
可換環論、コーエン・マコーレー、ゴーレンシュタイン環、表現論
- 研 究
テーマ -
- 可換ネーター局所環の表現論
研究活動の概要可換環の表現論について研究を行っています。特にゴーレンシュタイン環上の極大コーエン・マコーレー加群のなす圏について興味があり、その安定圏が三角圏になることなどの性質を用いて研究を行っています。
研究の方法としては、ゴーレンシュタイン環上の極大コーエン・マコーレー加群のなす安定圏において、それに属する傾加群を探し、その自己準同型環が持つ性質について調べています。
- 希望する
連携内容 -
- 可換環の表現論に関する分野
-
理学部 基礎理学科
- 教授
伊 代 野 淳
- 研究分野
素粒子天文学
- キーワード
高エネルギー宇宙線、高エネルギー宇宙物理
- 研 究
テーマ -
- 高エネルギー宇宙線原子核の組成の研究
- ガンマ線天体の研究
- 流星・火球の研究
研究活動の概要

高エネルギー宇宙線の起源、加速メカニズム並びに伝播の謎を解き明かすために、宇宙線空気のシャワー観測実験によるデータ収集を行い、理論モデルに基づくシミュレーション結果との比較考察を行っています。また、太陽活動による宇宙線の影響についてモニタリング観測を行っています。研究方法としては、本学校内並びに全国の共同研究機関に設置した宇宙線空気シャワー観測装置によって、宇宙線の到来時間、到来方向とシャワーサイズのデータを蓄積することで行っています。
また近年は気球搭載型原子核乾板ガンマ線望遠鏡を用いた高エネルギーγ線天体現象の研究並びに、HIMAC重粒子ビームを用いた宇宙線原子核同定のための低感度化原子核乾板の開発と、それによる宇宙線重原子核組成の研究を行っています。2015年、2018年にはオーストラリアでの気球実験に成功し、データ解析を行っている。また、2022年にスケールを一桁大きくした気球実験を計画している。
- 希望する
連携内容 -
- 放射線測定器の開発
- 原子核乳剤の開発
- 原子核同定のための固体飛跡検出器の開発
-
理学部 基礎理学科
- 教授
鎌 滝 孝 信
- 研究分野
堆積学、自然災害科学、防災・減災教育
- キーワード
地層科学、津波堆積物、自然災害、古環境
- 研 究
テーマ -
- 津波堆積物に基づく津波履歴の解明
- 津波および洪水堆積物に基づく災害評価に関する研究
- 堆積相や化石相に基づく古環境解析
- 防災・減災教育 など
研究活動の概要

我が国は沿岸部に広がる低平地に人口が集中しており、そのような場所における津波や洪水といった水災害の頻度や規模の将来予測に関する技術を高度化することは、人口集中地域における防災対策を進める上で重要な課題のひとつといえます。我々は、主に日本海沿岸を対象に、地球科学的手法で過去に発生した津波の痕跡をみいだし、その時間的・空間的分布を調べ、対象地域における過去の津波や洪水による浸水範囲やその発生時期を明らかにする研究をおこなっています。これらの研究成果は、沿岸低地における水災害リスク評価の高度化に役立つ情報を提供します。例えば、沿岸低地における津波と洪水による影響範囲や頻度を復元し、それらの成果を公表しハザードマップ等に過去の津波と洪水の浸水域を両方表現することができれば、そこで生活する住民にとっても防災意識の高揚につながる等、社会的な波及効果も大きいと考えます。
地震、津波や洪水に関する防災・減災教育実践やその普及、啓発活動にも積極的に取り組んでいます。- 希望する
連携内容 -
- 津波堆積物や洪水堆積物の調査、研究
- 地質調査、災害調査
- 防災・減災教育 など
-
理学部 基礎理学科
- 教授
齋 藤 達 昭
- 研究分野
環境科学、分子生物学
- キーワード
動植物の選好性、生態調査、ミトコンドリアDNA分析
- 研 究
テーマ -
- 岡山県旭川流域に生息する魚類などの個体群調査、生息環境条件の解明
- 植栽による閉鎖性水域の水質浄化
研究活動の概要
個体群調査では、標識再捕獲法で個体群の大きさを推定したり、耳石の輪紋から年齢を推定し、標準体長と年齢の関係を調べ、個体群の年齢構成を明らかにしています。
河川の水質や底質などの物理・化学的な条件を測定し、その生物がすみやすい環境条件を推定しています。
系統地理学的な研究では地域間における形態的あるいはミトコンドリアDNAの塩基配列などの相違を明らかにし、その生物の地理的な分布との関連性を調べています。
水草の植栽による岡山城の内堀の水質浄化に関する研究を行っています。
- 希望する
連携内容 -
- 水草の植栽による閉鎖性水域の水質浄化に関する分野
-
理学部 基礎理学科
- 教授
杉 山 裕 子
- 研究分野
分析化学、陸水学、地球化学
- キーワード
質量分析、溶存有機物、キャラクタりゼーション
- 研 究
テーマ -
- 天然水に溶存する有機物の構造、機能に関する研究
研究活動の概要

溶存有機物は、全ての陸水に数mg/Lから数百mg/L含まれるユビキタスな物質群で、地圏においても、水圏においても主要な炭素のリザーバーである。主に粒子状有機物の分解により生成する溶存有機物は、バクテリアの主要なエネルギー源であり、太陽光の入射を制限することで、水圏における一次生産や紫外線阻害などに影響を及ぼし、物質循環を直接的・間接的に支配している。それに加え、錯生成や吸着作用などにより他の微量溶存成分の水中での安定性をもたらしている。このように、天然水中の溶存有機物は様々な機能を有し、水質を決定付ける重要な因子であるが、分子種や構造などに関する情報は今なお限られている。
杉山研究室は、三次元励起蛍光スペクトル分析、フーリエ変換イオンサイクロトロン共鳴型質量分析、核磁気共鳴スペクトル分析などを用いて、天然水中溶存有機物を分子レベルで特徴づけ、分子種・化学構造や機能を明らかにすることを目的に研究を行っている。- 希望する
連携内容 -
- 溶存有機物の定性定量









